[!Tip]
随着我们设计越来越深的网络，深刻理解“新添加的层如何提升神经网络的性能”变得至关重要。

定义

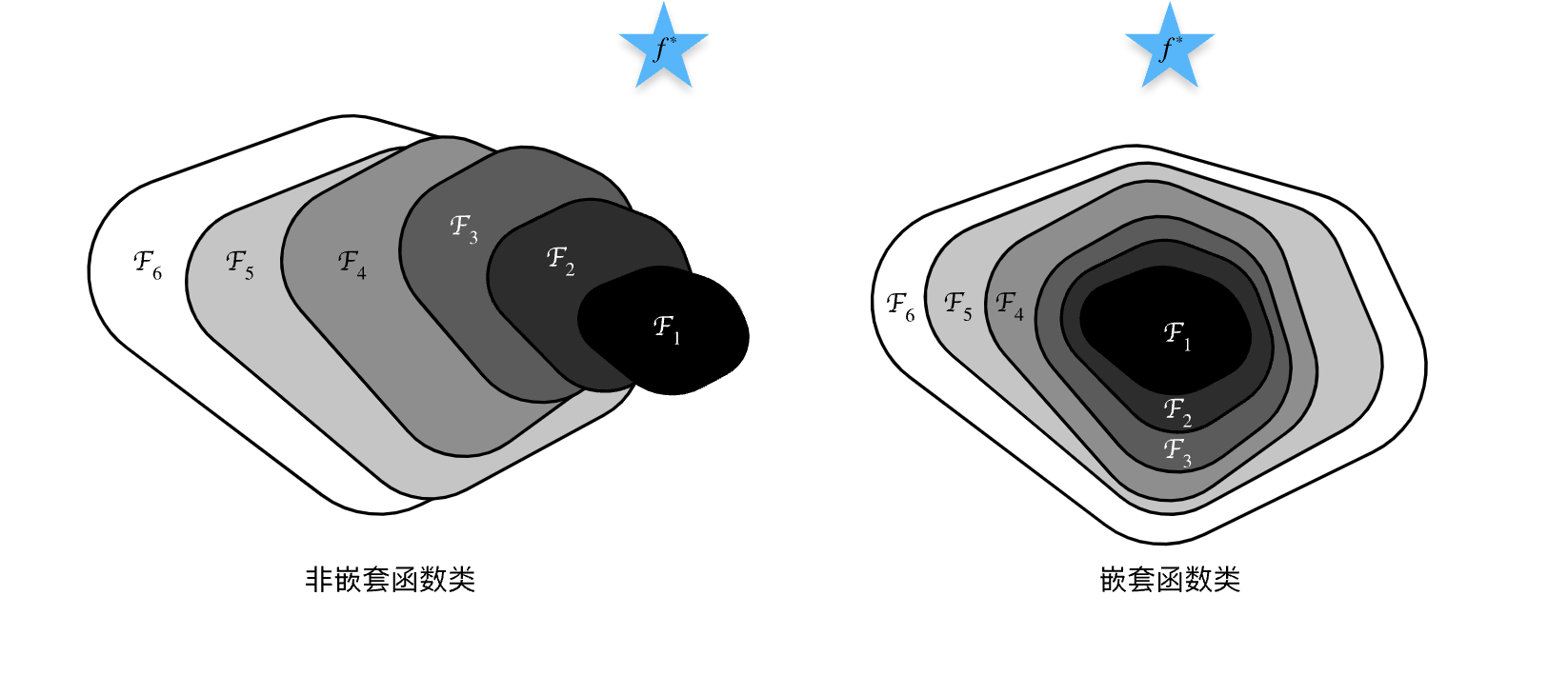
函数类

$f^*_\mathcal{F} := \mathop{\mathrm{argmin}}_f L(\mathbf{X}, \mathbf{y}, f) \text{ subject to } f \in \mathcal{F}.$

• $\mathcal{F}$ 是某种神经网络架构（包含超参数和学习率等），我们许要找的一个 $f^_\mathcal{F}$ 函数最接近目标函数 $f^$
• 如果要升级网络结构到 $\mathcal{F}’$，且 $\mathcal{F} \not\subseteq \mathcal{F}’$ 就会出现问题
  • 因此，只有当较复杂的函数类包含较小的函数类时，我们才能确保提高它们的性能。
  • 所以设计了残差网络，附加层要能包含原始网络
    

残差块（residual block）

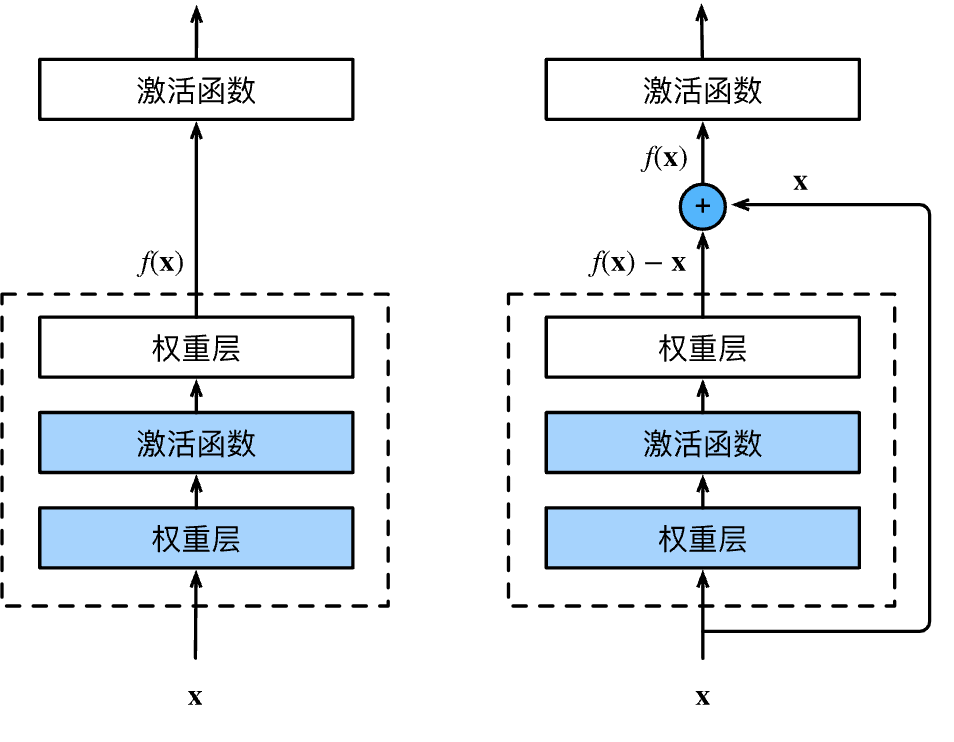
$f(\mathbf{x}) = \mathbf{x} + g(\mathbf{x}).$