李宏毅机器学习
【1】工作区/计算机/人工智能/学习/李宏毅课程/Pytorch 和 Colab 之后可以具体学习一下
反向传播等训练用到的原理可以滞后再看,先学习模型特性和推理本身
超参数
- 学习率
- 每层神经元数量
- 神经元层数
- Batch Size(计算速度和优化两个维度)
- RMSProp 梯度重要性参数
- 网络结构
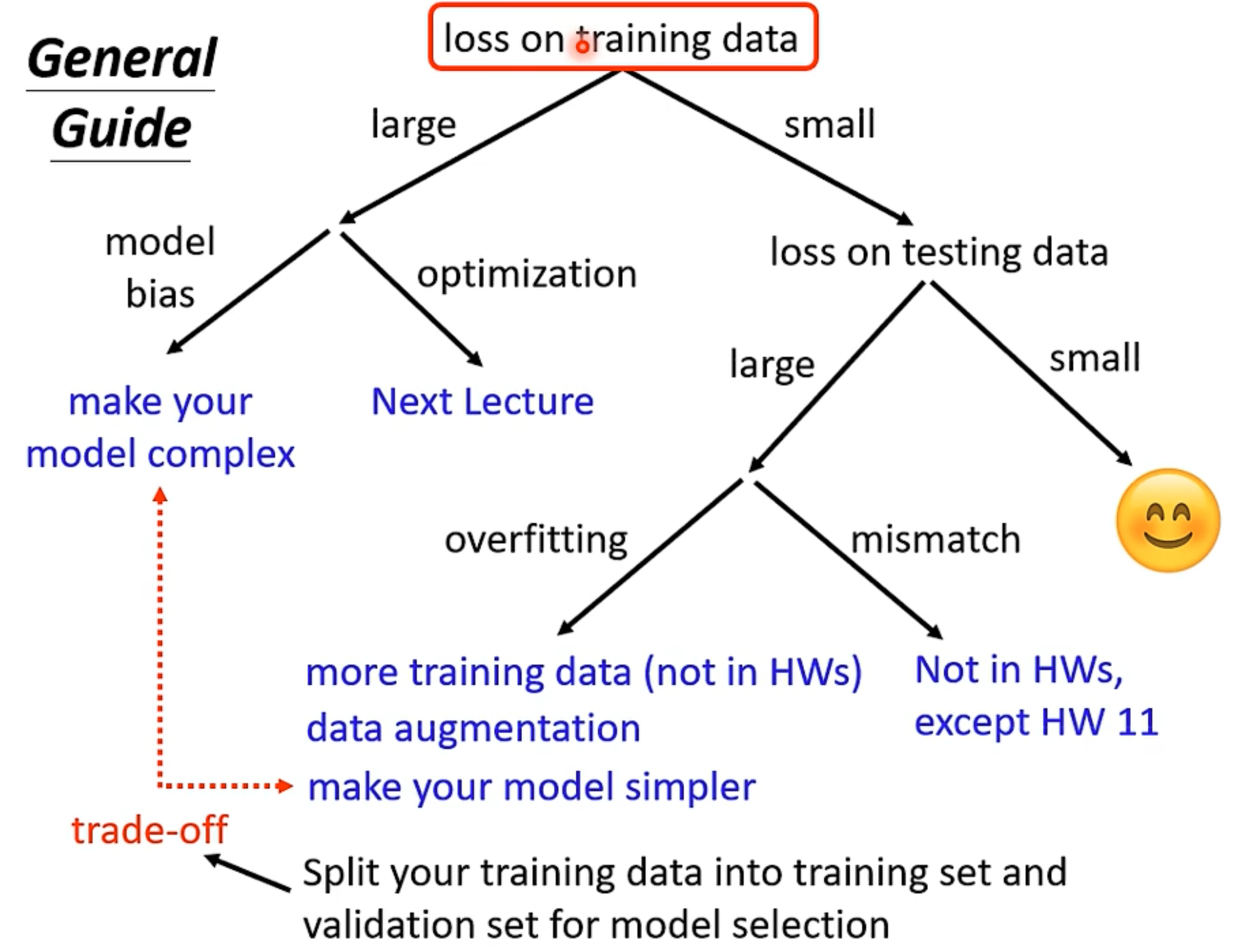
需要评估测试,在调整超参数会有怎样的变化,可以做出表格,对比曲线(本质就是实验),最简单是找出过拟合点(因为一开始目标是解决欠拟合,但是不断拟合会有对新数据预测能力变差的过拟合)
很多产出是经验,所以这个学科还在不断探索
模型偏差 Model Bias
预测模型的提升,参考数学建模 ,对模型进行优化,即考虑更多的实际情况,增加考虑的自变量/特征/feature(input 神经元个数)使权重变为矩阵;就是全连接层的雏形;即 $\bf{z=Wx}$
sigmoid 函数的意义(累加叠加的近似函数)
多个 sigmoid 和相当于是多个神经元(考虑某个连续函数曲线是由多个 sigmoid 函数合成近似);总之就是后面层某个神经元本质可能是一个目标函数(用 上一层的多个 sigmoid 输出合成的)也就是激活;sigmoid 可以替换比如 ReLU (但是需要两个 偏移正负相加得到 hard sigmoid)
思路:piecewise linear 不能近似复杂曲线 => 多个 hard sigmoid 合成 => sigmoid + weight + bias + constant
单层神经网络:
$y=b+c^T,{\sigma(b_i+\bf{W_ix})}$ c 通过转置变为行向量
最后函数变为 $F(x,\theta)$ (即神经网络函数),$\theta$ 是上面所有参数的集合;同理损失/代价函数就变为 $L(x,\hat{y},\theta)$ ,其中 $\hat{y}$ 为实际值/标签/label
然后变为一个优化问题 $\theta^*=arg,,min_{\theta}L$ ,通过梯度下降 g 更新参数(随机分 batch,即局部的梯度下降/Update,不同的 epoch 会 shuffle 各个 batch,实际 batch size 取决于计算立力,大小很有讲究:小的 size 对训练和测试反而更有帮助)
当 Loss 到达极限时候,加入多层神经网络可以优化结果
为什么需要 Deep 而不 Fat?
误差曲面(error surface):损失函数的图像
优化失败
临界点
梯度为 0,可能在局部极值(local minima)或鞍点(saddle point),即 critical point(临界点)
鞍点是可以继续去优化的
区分: 先泰勒展开到二阶(hessian 矩阵),通过二阶导数来判断是否为局部极值(首先二阶导数是函数的近似(因为梯度为 0,如果正定/特征值全部大于 0=>则该点为最小,负定/特征值全部小于 0=>最大值,不定则说明有时候大有时候小,就是鞍点)
可以用特征向量 u 和 hessian 矩阵得出优化方向,当移动方向为特征值小于 0 的特征向量时,二阶结果会小于 0(根据特征向量定义可得出),即找到下降方向(当前点向量加上改特征向量);但计算量很大
local minima 可能是高纬 saddle point 的投影;经验上是支持这种说法的,一般神经网络参数就很多
进一步优化
Batch Size 过小可能可以跨越一些 bad local minima,不容易造成 training 和 testing 的偏差过大
Momentum 的引入:考虑物理世界的惯性(有可能跨过一些局部最优),目标移动向量是当前动量加上负梯度的综合考量,多了一个超参数
对于动量的计算则是一个累积和;过去负梯度的累积和;
多学习率
loss 不下降不一定是梯度变小了
临界点其实很难走到,要特殊的梯度下降才能走到,也就是说真正影响 loss 的是其他因素
Adam 算法:RMSProp + Momentum
可能需要对参数使用不同的学习率(陡峭要小,平坦要大),需要给学习率加一个除数(依赖于不同参数和不同迭代次数两个维度;
- 只考虑不同迭代维度(Root Mean Square | Adagard):可以取之前梯度的平方平均值的平方根 $\sigma=\sqrt{\frac{1}{n+1}[\sum,(\bf{g}_i^{(L)})^2]}$);
- 考虑参数不同时候(RMSProp:找不到论文):多考虑了每次累加梯度时的重要程度,$\sqrt{\alpha(\sigma_i^{(L)})^2,+,(1-\alpha)(\bf{g}_i^{(L)})}$)
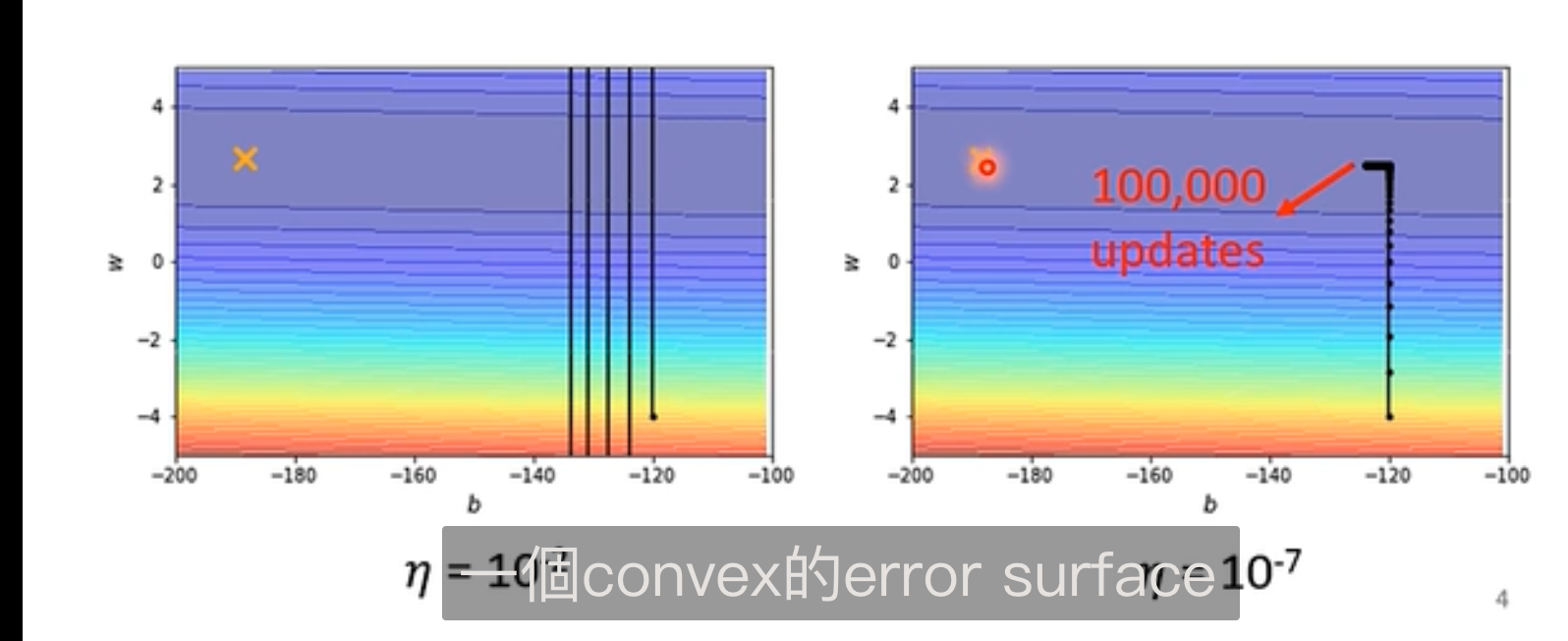
其中(Adagard)可能会梯度爆炸(出现 90 度大转弯,另外一个方向的梯度很小导致学习率会突然变大)
解决:
- 学习率规划(Learning Rate Scheduling):加上时间参数(随时间增加学习率变小 – 接近终点)
- Warm Up : 先变大,再变小;经验总结;很常见的黑科技;解释是 $\sigma$ 一开始是不精准的,统计信息少,所以学习率从小开始
加入动量则把梯度换成动量即可
分类
数据要独热编码:让各个 feature 不相关,几何距离相等
和回归的主要区别就是 label 是一个向量
softmax
正常值(logit)到 0-1 (normalization)的一个标准化。
具体原因需要再补充(可以看专门的讲解)
简单操作如下图
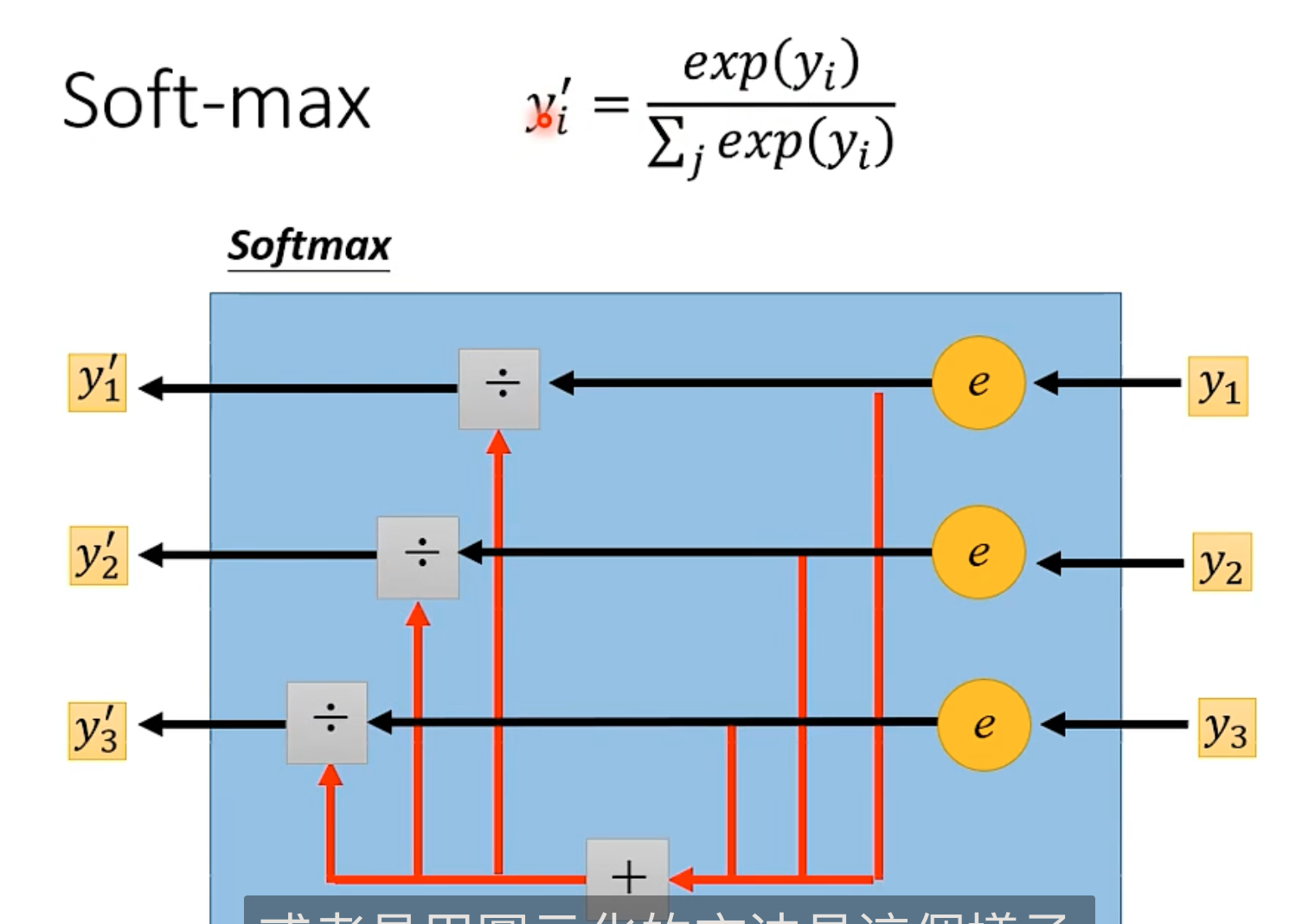
最终输出的结果和是 1,用了指数分布。
当两个 class 时可以直接用 sigmoid(等价)=> 逻辑回归
回归计算 loss 时候常用 MSE (均方误差),这里还可以用 Cross-entropy (交叉熵),更常用,并且和 softmax 绑定在一起(pytorch 会自动增加 softmax 到最后一层)
公式:$e=,-,\sum{\bf\hat{y}_i , \mit{ln} \bf{y_i^{’}}}$
error surface 区别:
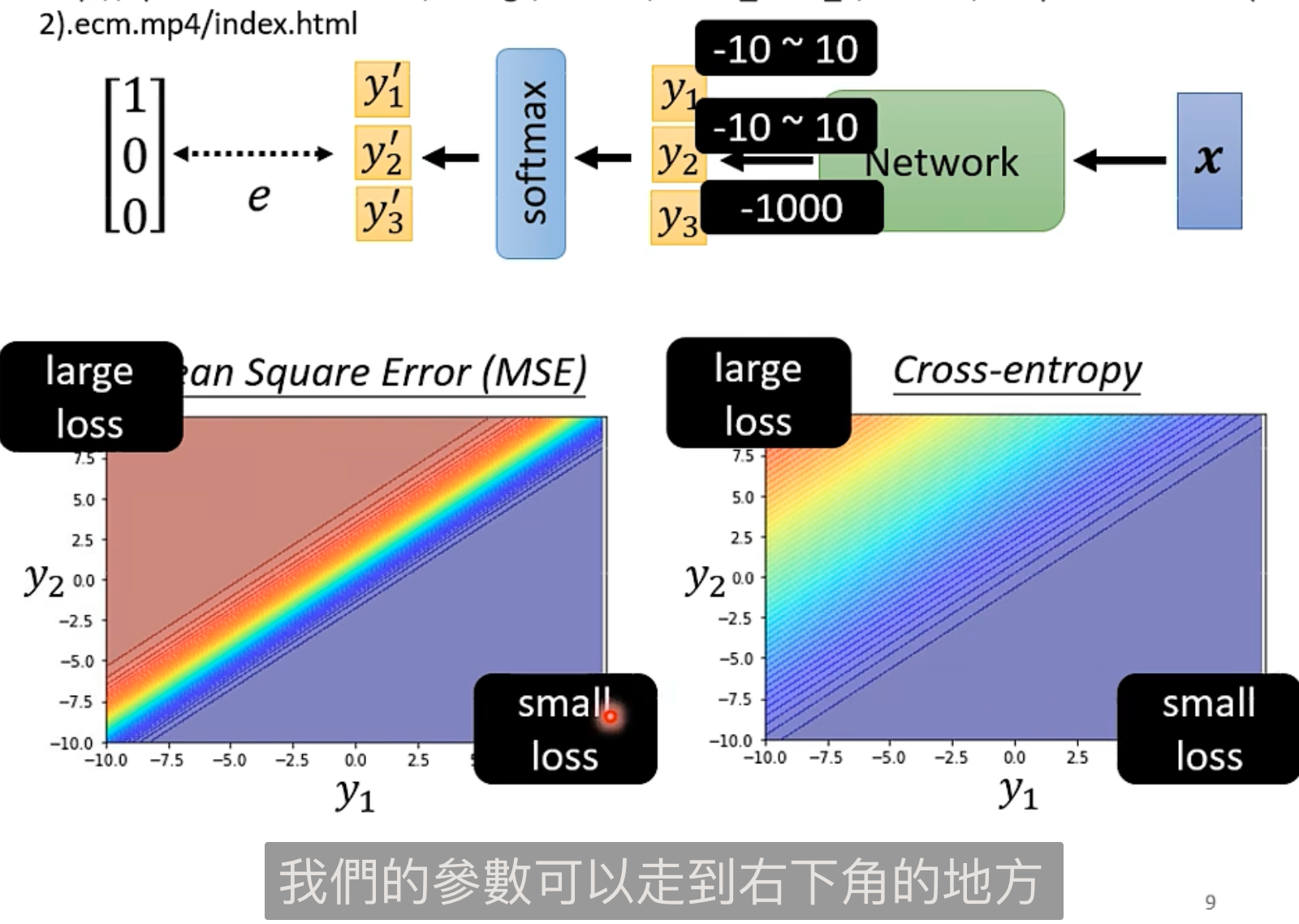
可以看到交叉熵的曲面会在 loss 大的时候会更平滑,说明修改 loss 可以让训练变简单
批次标准化(Batch Normalization)
“铲平误差曲面的山”
最佳实践 Internal Covariate Shift :
input feature 差距很大会产生山(因为不同纬度对损失函数的变化程度差距大)
所以需要 Feature 标准化到 0-1 之间:$\widetilde{x}_i^r,\leftarrow,\frac{x_i^r,-,m_i}{\sigma_i}$
$\sigma$ 为标准离差(对于样本均值的一阶中心矩),就是概率论里面的归一化
这样会让梯度收敛得更快,同理在 z 或者 a 处也能做 Normalization。
如下:本质是让单个输入能影响到其他部分的内容,单个神经元的计算变成了更大的网络
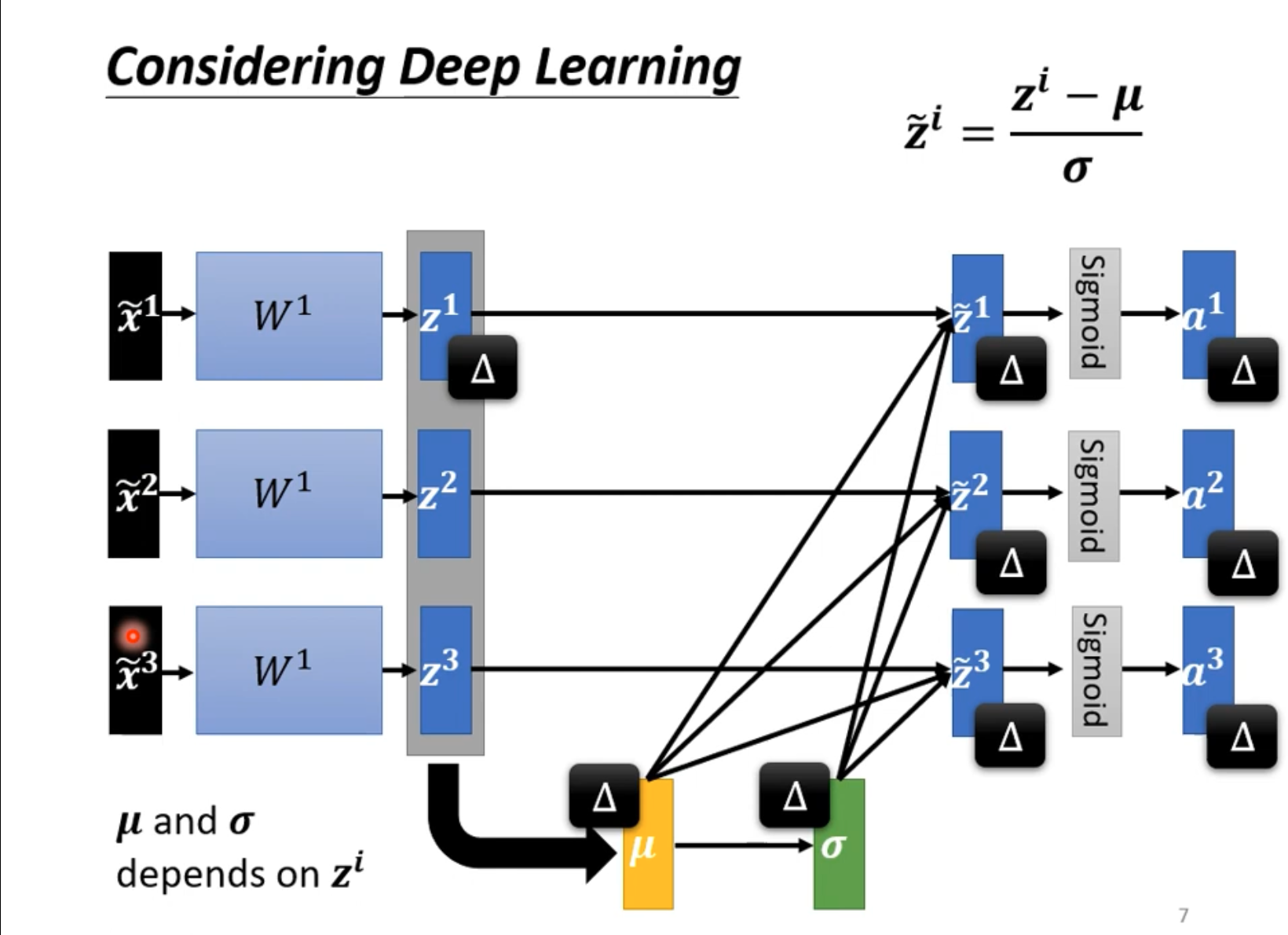
如此每个 batch 才往 GPU 里送东西
进一步,批次的标准化:其中新参数是模型的参数,前面标准化的参数是计算出来,而这部分是训练出来的(初始化为 1 和 0,保证各部分都是相近的);用途?(待理解)

测试的情况
数据不足时如何标准化?
解决:训练阶段记录 $\mu^{(L)}$,然后计算 Moving Average (平滑插值) $\bar{\mu},=,p\bar{\mu},+,(1-p)\mu^{(L)}$
Pytorch 中会自动计算这个
CNN 卷积神经网络
对于图像处理本身是很大一块:到神经网络输入,图像至少要是同样的维度输入。所以对图像进行卷积,每个神经元的计算不再是所有元素的一个矩阵变换,而是观察一个部分区域。(这里面卷积的思想很值得思考,参考 3b1b)
分类需要独热编码
但是图像输入很大(如果是一般全连接层),所以需要提取特征:也就是 3b1b 中对手写识别的说法(图片由许多组成部分得到)
Receptive Field 接受域
CNN 会设置 Receptive Field 接受域,如此每个后续神经元只需要输入的部分做连接。
如何确定连接(即 Receptive Field)?
答:是可设计的,根据需要选取。
对于一般的模型方式:
- 选取 all channels
- Receptive Field 平面大小做作 kernel size,一般 3x3
- 通过 kernel 移动产生新的 Receptive Field 的移动(水平或垂直)参数叫做 stride (尽可能多重叠),超出边缘的情况用 padding,即补零
共享参数
对于不同 Receptive Field 但是识别相同内容的神经元需要共享参数去减少训练参数数量。
共享的参数叫做 Filter,size = 3x3 x channel
以上两个特性总结起来就是卷积神经网络,即做了两层限制,增大 Model Bias(但是在影像识别上不会有太大影响 )。
另一个视角
具体实现,因为需要共享参数(Filter 去扫图片是一种共享参数),所以是以 Filter 为导向去处理 Input 的,也就是卷积操作(参考高斯模糊做的的事情,卷积本身是一种模糊,可以回顾 3b1b,看看能不能思考清楚本处的本质意义)。
结果会得到一个 Feature Map,变成一张新图片,其中 channel 从 RGB 变化为 Filter 的数量,即卷积的次数。
所以安排 CNN 网络层时需要考虑前后 channel 的变化。
这样的结果会导致一个后续的 CNN 层,用同样大小的 Filter 本质看到了更多的东西。
Pooling 池化
一个新的视角,做下采样(subsampling),不是一个网络层,像是一个激活函数。
Max Pooling
在 Feature Map 中分区,然后选取最大作为代表,把图片变小,减少算力,但是会有损失,所以在精细的识别中不能用。
Flatten 压扁
把矩阵拉直为向量,然后能继续放到全连接层中去。最后在经过 softmax 然后得到分类结果。
围棋的应用
棋盘被当作一张图片,而某一个子在该位置各种不同的意味作为 channel。
这是因为棋盘问题和图片识别问题本质是一样的
问题
不能处理放大缩小旋转的问题,所以要做 data augmentation(数据增强),预先对数据进行处理
自注意力 Self- Attention
Input 变为一排向量?且数量可变?
输入是一个 Sequence of Vector
时间序列分析
例子:
- NLP,单词序列编码;使用词嵌入代替独热编码,因为词之间有相关性
- 声音,采样可以用一个向量表示,采样就逐渐往后偏移(中间会有重合)
- Graph(社交网络,分子模型),图忘了也是一个向量(邻接矩阵)
Output
- 每一个 Vector 有一个 label 输出:文字处理(POS Tagging:词性标注),音标识别,社交网络(推荐系统)
- 唯一 Label 输出:文本分析(情感分析,正负面评价),语音识别(辨识说话者),分子性质(毒性,亲水性)
- seq2seq:多对多输出 ,语言翻译,语音辨别
因为同样的输入,不一定等幂,可能和过去有关,即时间序列(同一个词,不同词性)。
全连接层可以做量级少的前后连接分析 *(?好像是把 Input 的向量串起来)
所以引入 Self-attention(综合了序列其他内容,和 Transformer 有关,参考 Attention in your need Paper);输出多方面考虑的输入向量给全连接层。
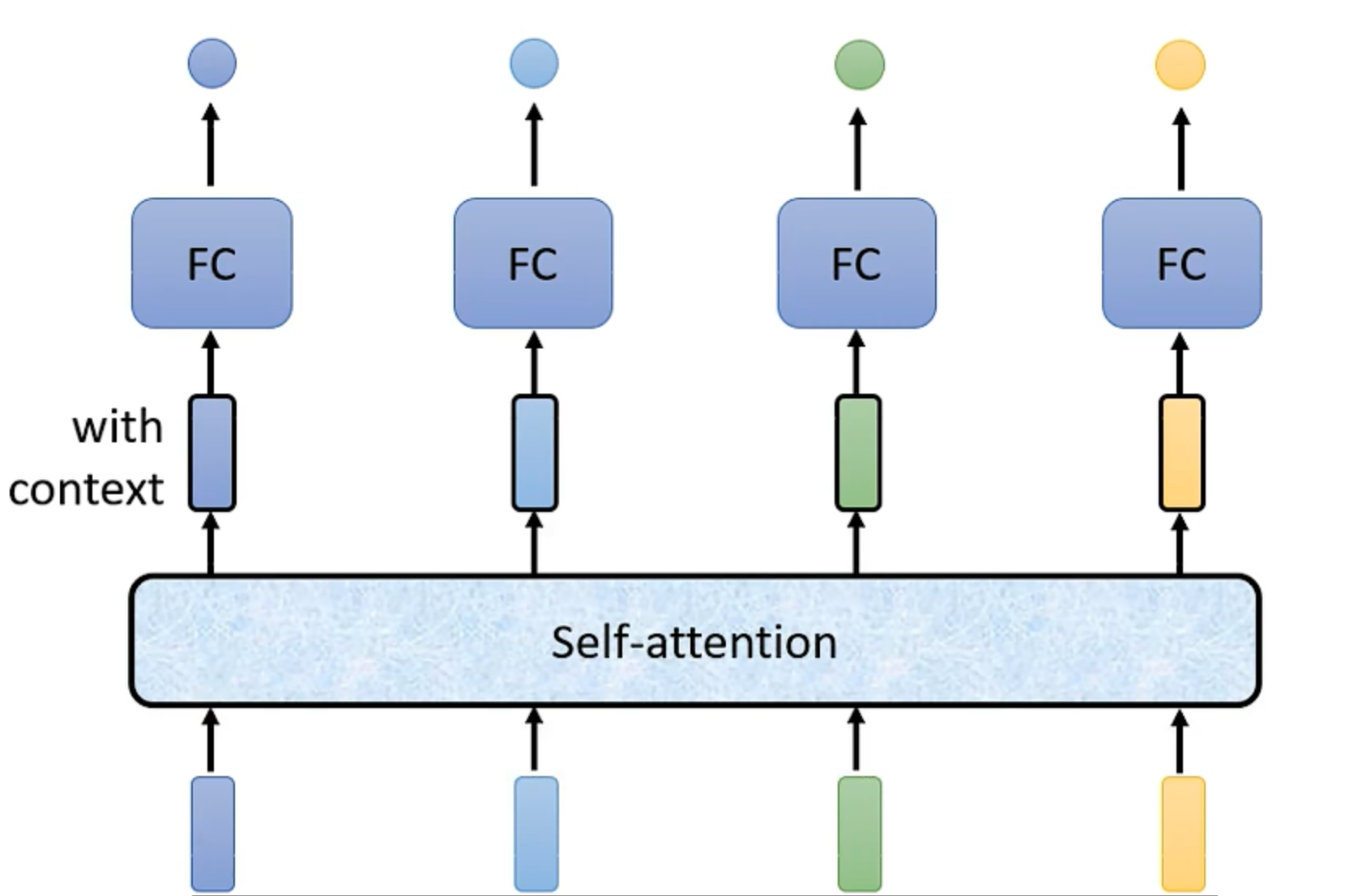
可以叠加多次,具体看需求选择(参考 CNN 的其他应用,主要是考虑这个概念的特性)
Self-attention 结构
输入是一系列向量
分析一个输入与其他输入的相关性,用 $\alpha$ 表示,称为 Attention Score
任意两个输入需要一个计算 Attention 的 Module(输入为两个向量,结果为相关度)
计算相关程度
相关度分析方法(都要先用两个 W 矩阵转换为另外两个向量,即可学习的参数):
- 点积:结果作为相关度(transformer 中用到)
- 相加:再做 tanh 最后用一个矩阵 W 输出相关度
- …
计算样例如下:

其中自己可以和自己做分析,即 a1 自己再做一个 key 的生成然后计算关注分数
所有的 $\alpha$ 可以做一个 softmax(化为指数分布);
计算结果
根据 Attention Score 计算出 Self-Attention 的 Output
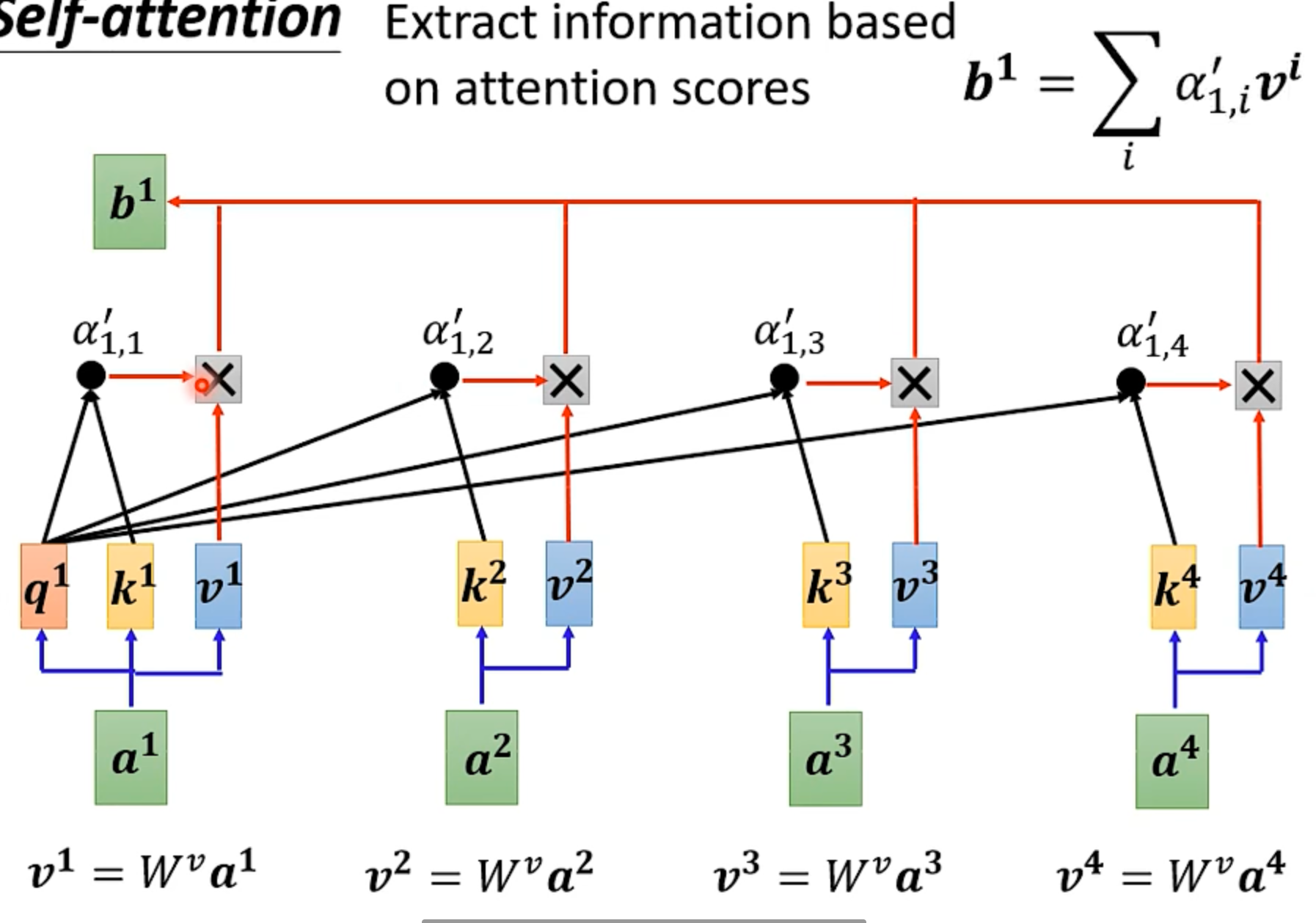
根据计算特性,这个部分可以并行计算。
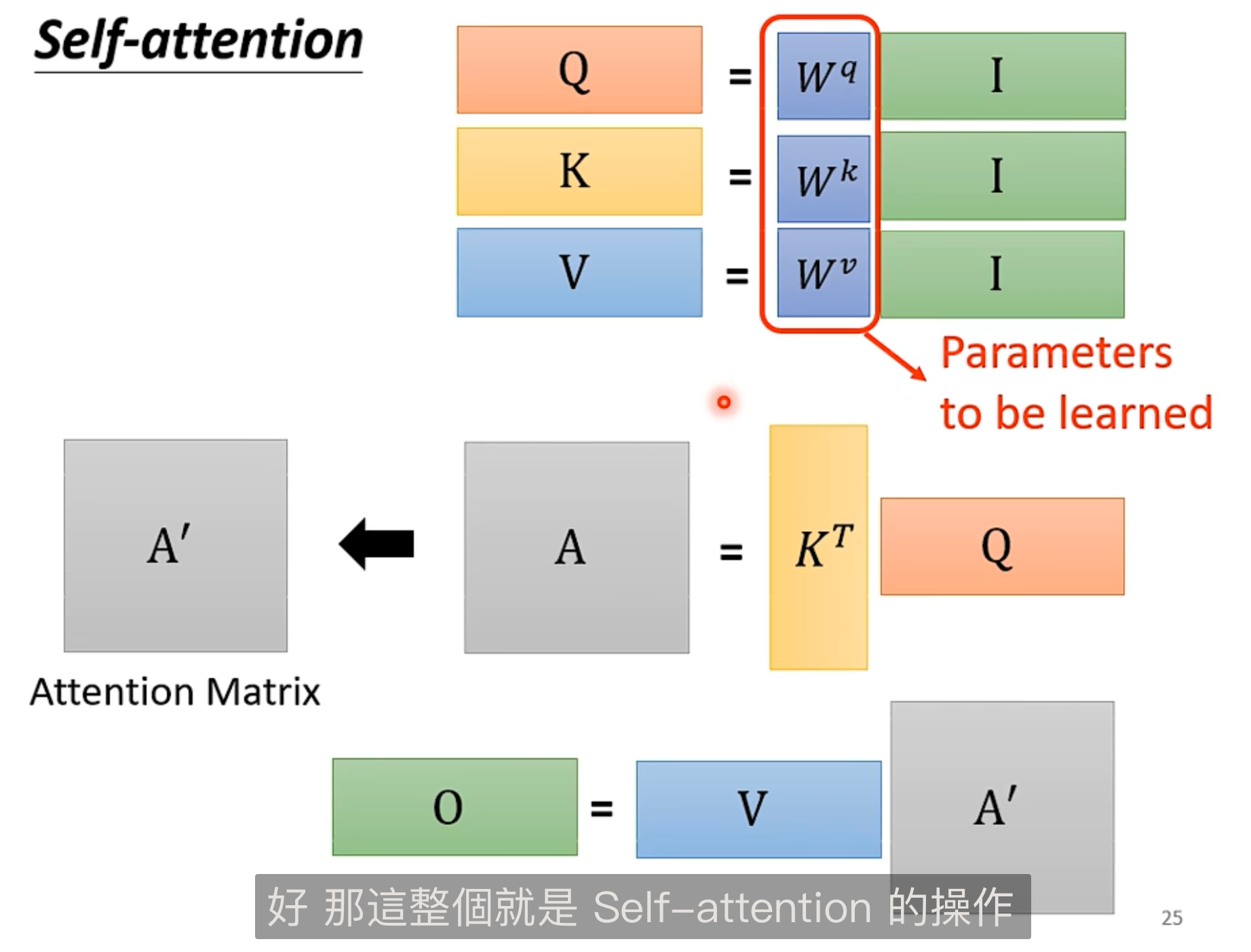
矩阵化:
- q 的计算:$\bf{Q},=,\bf{W}^q,\bf{I}$ 其中 $\bf{I}$ 是由 $a^i$ 构成的矩阵
- 同理有 k 的计算:$\bf{K},=,\bf{W}^k,\bf{I}$
- v 的计算:$\bf{V},=,\bf{W}^v,\bf{I}$
- 相关度计算:$\bf{A},=,\bf{K}^T,\bf{Q}$ 每个 q 都要和其他几个 k 做点积
- Soft max: $\bf{A},\rightarrow,\bf{A}^{’}$
- 计算输出:$\bf{B},=,\bf{V},\odot,\bf{A}^{’}$

Multi-head Self-Attention
q 计算环节通过多个矩阵得到更多的 q,即 head;同时,k,v 也要增加运算,即多一个矩阵运算
最后输出时,通过一个新的矩阵 W 变化为一个输出
位置编码
需要对位置信息的考虑,才有序列的思考
positional encoding(人为考虑): 增加一个位置向量 $e^i$ 加到输入向量中
Transformer
GAN
VAE
自解释方法
t-SNE
预先:需要懂得 PCA
非线形降维
非欧空间拉直,然后可以降维用 Euler Distance